• STL Vector
우선 STL이란 Standard Template Library(표준 템플릿 라이브러리)의 약자이다.
C++ 언어로 프로그래밍 하는데 필요한 자료구조와 알고리즘을 제공해준다.
Vector는 STL의 컨테이너 중 하나로, 동적 배열을 나타낸다.
Vector의 연산은 다음과 같다.
#include <vector>
std :: vector<data_type> name; // vector 선언
std :: vector<data_type> name(size);
name.size() // std::vector의 요수 수 반환
name.empty() // name이 비어있는지 확인
name.push_back() // name 끝에 요소 추가
name.pop_back() // name 끝에 있는 요소 제거
• STL Stack
용량 제한이 없고 템플릿 기반이다.
STL Stack의 API는 다음과 같다.
#include <stack>
std::stack<data_type> name; // 객체 생성하기
void name.push(data_type x); // 스택의 맨 위에 새로운 요소 삽입
void name.pop(); // 맨 위의 요소 제거, 반환 X
data_type name.top(); // =peek() 맨 위의 요소 반환, 제거X
int name.size(); // 스택의 크기 반환
bool name.empty(); // 비어있는지 여부 판단
• 수식 계산
Input : +, -, /, * (사칙연산)
Output : 주어진 수식의 연산 결과
ex) 2 + 3 * 4 = 14
용어 정리
- Operator (연산자) : +, -, /, *
- Operand (피연산자) : 2, 3, 4
- Infix notation : 연산자가 피연산자 사이에 존재한다. (2 + 3)
- Prefix notation : 연산자가 피연산자 앞에 존재한다. (+ 2 3)
- Postfix notation : 연산자가 피연산자 뒤에 존재한다. (2 3 +)
Infix notation이 사람이 보기에는 편하지만, 컴퓨터는 아니다.
따라서 Infix를 Postfix로 변환하는 작업을 해주어야 한다.

수식 계산의 단계이다.
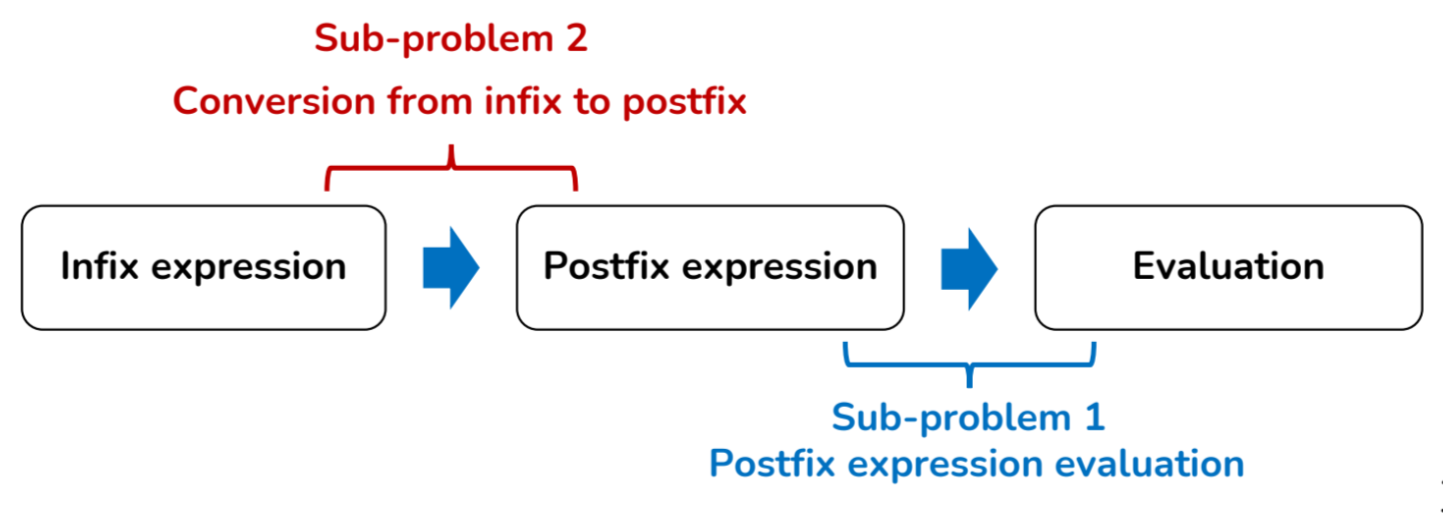
• Postfix Expression Evaluation(Postfix 계산)
올바른 입력이 주어졌다고 가정한다.
Postfix Expression Evalusation의 Main idea는 Stack의 LIFO이다.
따라서 마지막으로 등장했던 두개의 피연산자가 무엇인지 알아보는 것이 중요하다.
- Step 1-1. 현재 항목이 피연산자인 경우, 이를 스택에 push한다.
- Step 1-2. 현재 항목이 연산자인 경우,
스택에서 항목을 pop하여 두 번째 피연산자로 설정한다.
그 다음을 항목을 pop하여 첫번째 피연산자로 설정한다.
첫번째와 두번째 피연산자를 계산한 후 다시 스택에 push한다.
여러개가 있거나 아무것도 없으면 잘못된 연산이다.
Postfix가 올바르게 진행되었다면, 오직 하나의 값만 스택에 남아있어야 한다.

슈도코드로 표현하면 아래와 같다.
def calc_postfix(expr):
# 스택 생성
st = stack (double-typed stack)
# 표현식의 각 항목에 대해 반복
for term in expr:
# 피연산자인 경우
if term is operand:
st.push(term) # 스택에 피연산자를 추가
# 연산자인 경우
else if term is operator:
op = term # 연산자를 가져옴
# 스택에서 두 번째 피연산자와 첫 번째 피연산자를 꺼냄
second = st.pop()
first = st.pop()
# 연산을 수행하고 결과를 스택에 추가
result = first op second # op ∈ {+ - * /}
st.push(result)
return st.pop()
• Infix to Postfix
이 과정은 조금 더 복잡하다.
연산자 우선순위
( or ) => 0
+ or - => 1
* or / => 2
괄호는 우선순위가 제일 낮다.
스택 상단으로 올라갈수록 우선순위가 높아진다.- 피연산자(operand)인 경우:
현재 항목이 피연산자인 경우, 이를 후위 표기식에 바로 추가한다. - 연산자(operator)인 경우:
현재 항목이 연산자인 경우, 다음 단계를 따른다.
- 스택의 맨 위의 연산자와 현재 연산자의 우선순위를 비교한다.
- 스택이 비어있거나 현재 연산자의 우선순위가 더 낮은 경우, 현재 연산자를 스택에 넣는다.
- 스택의 맨 위의 연산자의 우선순위가 더 높거나 같은 경우, 스택의 맨 위의 연산자를 후위 표기식에 넣고 스택에서 제거한다. 이 과정을 반복한다.
- 왼쪽 괄호(left paren)인 경우:
왼쪽 괄호인 경우, 스택에 넣는다. - 오른쪽 괄호(right paren)인 경우:
오른쪽 괄호인 경우, 왼쪽 괄호가 나올 때까지 스택에서 연산자를 후위 표기식에 넣고 스택에서 제거한다.
괄호는 후위 표기식에 넣지 않는다. - 모든 항목을 확인한 후:
스택이 비어있을 때까지 스택의 맨 위의 연산자를 후위 표기식에 넣고 스택에서 제거한다.

슈도코드로 표현하면 다음과 같다.
def infix_to_postfix(expr):
# 스택과 후위 표기법으로 변환된 표현식을 저장할 벡터 생성
st = stack
postfix = vector
# 표현식의 각 항목에 대해 반복
for term in expr:
# 피연산자인 경우
if term is operand:
# 후위 표기법에 피연산자를 추가
append term to postfix
# 연산자인 경우
else if term is operator:
# 스택이 비어있지 않고, 스택의 맨 위 연산자의 우선순위가 현재 연산자보다 높거나 같을 때까지 반복
while st is not empty:
if st.peek()’s priority ≥ term’s priority:
# 스택의 맨 위 연산자를 팝하고 후위 표기법에 추가
op ← st.pop() and append op to postfix
else: break
# 현재 연산자를 스택에 푸시
st.push(term)
# "(" 인 경우
else if term is "(":
# 스택에 "(" 추가
st.push(term)
# ")" 인 경우
else if term is ")":
# 스택이 비어있지 않은 동안 반복
while st is not empty:
# 스택에서 연산자를 팝
op ← st.pop()
if op is "(":
# "("를 만나면 중지
break
else:
# 후위 표기법에 연산자 추가
append op to postfix
# 스택에 남은 모든 연산자를 후위 표기법에 추가
while st is not empty:
op ← st.pop() and append op to postfix
# 후위 표기법으로 변환된 표현식 반환
return postfix
• Stack application
만약 잘못된 형태의 Infix가 주어지면 Postfix에서도 오류가 생성된다.
시간복잡도는 #5의 괄호 검사와 같은 방식으로 계산된다.
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] #8 Queue(2) (0) | 2024.04.21 |
|---|---|
| [자료구조] #7 Queue(1) (0) | 2024.04.21 |
| [자료구조] #5 Stack(1) (0) | 2024.04.16 |
| [자료구조] #4 C++ 문법(2) (0) | 2024.04.15 |
| [자료구조] #3 C++ 문법(1) (0) | 2024.04.14 |