• Stack
스택은 말 그대로 '쌓아놓은 더미'를 뜻한다.
스택의 가장 큰 특징은 'LIFO'(Last In First Out) 이다.
다시 말해, 가장 최근에 들어온 데이터가 가장 먼저 나간다는 의미이다.

스택의 연산은 top(상단)에서만 진행된다.
주요 연산자
push : 삽입 연산
pop : 삭제 연산(삭제&반환)

• Function call stack

반복적으로 함수를 호출하는 무한 루프가 있는 경우 스택 오버플로우가 발생할 수 있다.
• 부가연산자
- peek() : 스택의 맨 위에 있는 데이터를 제거하지 않고 반환한다.
- empty() : 할당된 공간에 삽입된 아이템이 없을 때 반환한다. / 아이템이 한개라도 있으면 false.
- full() : 할당된 공간이 모두 채워졌을때 반환한다. / 공간이 남아있으면 false.
- size() : 원소의 개수를 반환한다.
• Array-based Stack(배열 기반 스택)
배열은 일반적으로 고정된 크기를 갖는다.
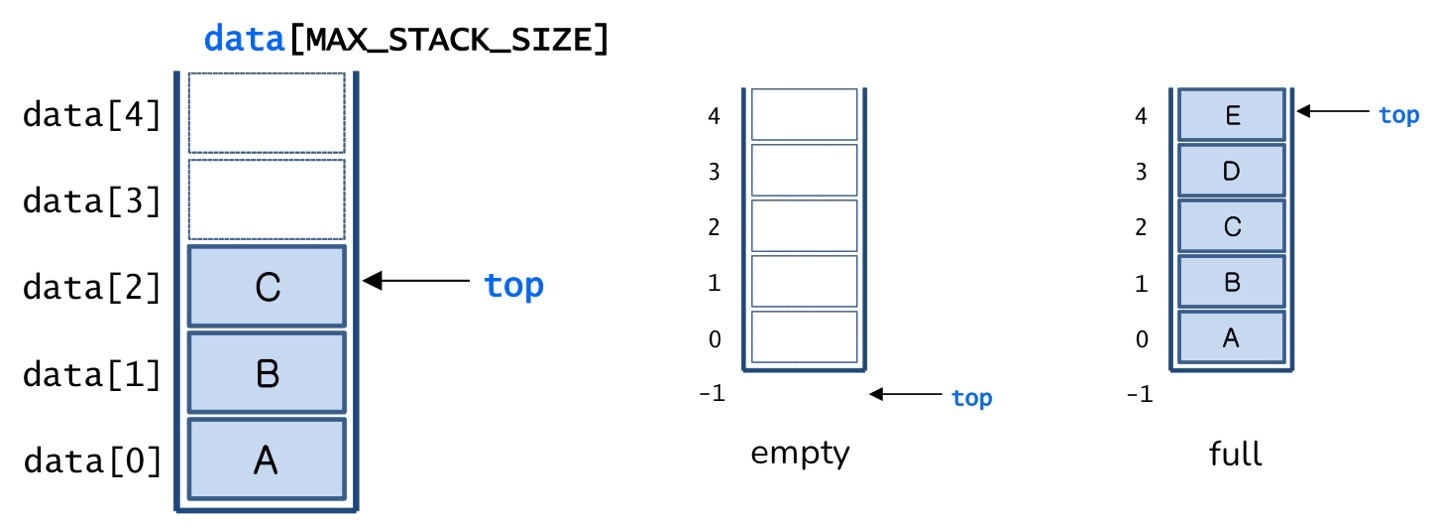
아이템 저장을 위한 배열 : data[0] ··· data[top]
만약 top이 -1이면, 스택은 empty이다.
만약 top이 MSS(data[MAX_STACK_SIZE]) - 1이면 스택은 full이다.
• Push 연산자
def push(x):
if full():
throw "stack is full"
else:
top <- top + 1
data[top] <- x
C언어로 시간복잡도를 계산해보면 상수시간에 연산이 수행된다는 사실을 알수 있다.

• Pop 연산자
def pop():
if empty():
throw "stack is empty"
else:
e <- data[top] // e에 저장
top <- top - 1
return e
이것도 동일하게 상수시간에 연산이 수행된다.

배열 기반 스택의 장점은 구현하기 쉽다는 것이지만
단점은 고정된 크기만큼만 아이템을 받을 수 있다는 것이다.
임의의 크기에 대해서도 받을 수 있게 하는 방법이 두가지 있는데,
1. 동적 배열을 사용해서 요소를 추가하거나 삭제할 때마다 자동으로 크기를 조절할 수 있다.
(시간복잡도 O(n))
2. linked list를 사용할 수 있다.
• 스택 클래스 디자인
바로 클래스를 구현하기 전에 다이어그램을 그리는 것이 좋다.

- : private / + : public
위 다이어그램을 보면,
첫번째 줄에는 'ArrayStack'이라는 클래스 이름
두번째 줄에는 'top'과 'data'에 해당하는 멤버 변수와 멤버 변수의 타입(int)
세번째 줄에는 멤버 함수와 return타입을 알 수 있다.
• ADT 구현
class ArrayStack
{
private:
static const int MAX_STACK_SIZE = 20; // 스택의 최대 크기
int top; // top을 나타내는 변수
int data[MAX_STACK_SIZE]; // 배열 저장
public:
ArrayStack() { top = -1; } // 생성자
~ArrayStack() {} // 소멸자
bool empty() { return top == -1; } // 스택이 비어있는지 확인
bool full() { return top == MAX_STACK_SIZE - 1; } // 스택이 가득찼는지 확인
int size() { return top + 1; } // 스택의 요소 개수 반환
void push(int e) {
if (full()) throw "stack is full";
data[++top] = e; // 스택에 요소를 추가해서 top 증가시킴
}
int pop() {
if (empty()) throw "stack is empty";
return data[top--]; // 스택에 요소를 제거&반환해서 top 감소시킴
}
int peek() {
if (empty()) throw "stack is empty";
return data[top]; // 스택의 가장 위에 있는 요소 반환
}
void display() {
cout << "# of items: " << size() << std::endl;
for (int i = 0; i <= top; i++)
std::cout << "[" << data[i] << "]" << std::endl;
}
};
• 스택을 이용한 괄호 검사
# left : [, {, (
# right : ], }, )
조건
C1. 왼쪽 괄호와 오른쪽 괄호의 개수가 일치해야 한다.
C2. 왼쪽 괄호(여는 괄호)가 오른쪽 괄호(닫는 괄호)보다 먼저 나와야 한다.
C3. 제일 먼저 나온 왼쪽 괄호(여는 괄호)에 대응되는 오른쪽 괄호(닫는 괄호)가 제일 나중에 나와야 한다.
따라서 괄호는 LIFO의 특징을 가지고 있는 것을 알 수 있다.
괄호를 Stack과 같은 형태로 두어보자.

우리는 스택을 통해 괄호 문제를 해결할 수 있다.
- 스택을 사용하여 왼쪽 괄호를 저장하여 어떤 왼쪽 괄호가 마지막에 오는지 확인한다.
- 오른쪽 괄호가 나오면, 스택에서 가장 최근에 저장된 왼쪽 괄호를 꺼내어 매칭 여부를 확인한다.
- 스택이 비어있는 경우, C2가 위배된다. ex) )a(b)c(
- 매칭되지 않는 경우, C3가 위배된다. ex) a{b(c[d}e]f)
- 모든 괄호를 확인한 후에도 스택이 비어있지 않으면, C1이 위배된다. ex) (a(b)
예시

위의 알고리즘을 분석해보자.
Step 1-1. 만약 왼쪽 괄호가 나타나면, push한다.(넣기)
Step 1-2. 만약 오른쪽 괄호가 나타나면, pop한다.(빼기)
만약 스택이 비어있다면, C1나 C2가 위배된 것이다.
Step 2. 왼쪽 괄호가 오른쪽 괄호와 대응하는지 보자.
만약 대응하지 않는다면 C3가 위배된 것이다.
마지막 괄호가 진행된 이후 스택이 비어있지 않다면, C1이 위배된 것이다.
반대로, 스택이 비어있다면 모든 괄호가 일치하는 것이다.
• 괄호 검사 알고리즘의 시간복잡도
입력 문자열의 길이를 n이라고 가정한다면,
worst case일 경우 시간 복잡도는 Θ(𝑛)이다.
증명:
- 모든 문자를 읽는 데 걸리는 시간 복잡도 : 𝑛
- 스택 작업(push 또는 pop)의 시간 복잡도 : 𝑚
- 따라서 𝑇(𝑛) = 𝑛 + 𝑚 ∈ Θ(𝑛)이다.
여기서 𝑚 ≤ 𝑛이므로, dominant factor은 𝑛이다. (𝑛은 모든 괄호의 수이기 때문이다.)
'CS > 자료구조' 카테고리의 다른 글
| [자료구조] #7 Queue(1) (0) | 2024.04.21 |
|---|---|
| [자료구조] #6 Stack(2) (0) | 2024.04.19 |
| [자료구조] #4 C++ 문법(2) (0) | 2024.04.15 |
| [자료구조] #3 C++ 문법(1) (0) | 2024.04.14 |
| [자료구조] #2 알고리즘 분석(2) (0) | 2024.04.11 |